striving & singing
2020-07-13 ~ 2020-07-16
因为要中考所以没刷题。
2020-07-17
关于最小生成树:
- 切割性质:将点集分为任意两个不相交的非空子集,则连接两个不同点集的点的最小的边一定在图的最小生成树中。
- 回路性质:原图的环上最大的边一定不在图的最小生成树中。
- 一个没有名字但常见的思路:把一条边加入到当前的生成树中形成一个环,若这条边小于环上最大的边则把最大的边去掉,加入当前边,形成的新生成树比原生成树小。
- 由上面得出的一个推论:原图的环上最小的边一定在图的最小生成树中。
走廊泼水节
https://www.acwing.com/problem/content/description/348/
对于树上的一条边,边的两侧是两个连通块,需要在两个连通块之间加边,使得每两个节点之间都有边。为了不破坏原有的最小生成树,所加的边的边权必须大于当前最小生成树的最大边,因此至少为当前边的边权加一。一条边对答案的贡献为$(w+1)\times(size_x\times size_y - 1)$。
对于为什么要从小到大扫描,网上的题解大多知其然不知其所以然。这个问题我想了半天,最后得出的结论是为了使答案最小。最小生成树不变已经在上面的操作中得到了保证,而从小到大扫描可以使答案最小。考虑不按照从小到大扫描,每次合并时加的边权是两个生成树中最大的边的边权加一,那么大的边更早地加入到最小生成树中,显然会使每次合并时的答案更大。为了使答案最小,大的边需要尽量晚地加入到最小生成树中。
#include<cstdio>
#include<algorithm>
int t, n, ans;
struct tools { static inline void swap(int &a, int &b) { int t = a; a = b; b = t; } };
struct edge {
int u, v, w;
bool operator < (const edge &a) const { return w < a.w; }
}edges[6010];
struct unionsetnode { int fa, size; };
struct unionset {
unionsetnode nodes[6010];
inline void init() { for (int i = 1; i <= n; i++) nodes[i].fa = i, nodes[i].size = 1; }
int find(int x) {
if (nodes[x].fa == x) return x;
return nodes[x].fa = find(nodes[x].fa);
}
inline void merge(int x, int y) {
x = find(x), y = find(y);
if (nodes[x].size < nodes[y].size) tools::swap(x, y);
nodes[y].fa = x;
nodes[x].size += nodes[y].size;
}
inline bool same(int x, int y) { return find(x) == find(y); }
inline int count(int x) { return nodes[find(x)].size; }
}uset;
int main() {
scanf("%d", &t);
while (t--) {
ans = 0;
scanf("%d", &n);
uset.init();
for (int i = 1; i < n; i++)
scanf("%d%d%d", &edges[i].u, &edges[i].v, &edges[i].w);
std::sort(edges + 1, edges + n);
for (int i = 1; i < n; i++) {
int &u = edges[i].u, &v = edges[i].v, &w = edges[i].w;
ans += (w + 1) * (uset.count(u) * uset.count(v) - 1);
uset.merge(u, v);
}
printf("%d\n", ans);
}
return 0;
}MST Company
https://www.luogu.com.cn/problem/CF125E
假设给出的是连通图。把与$1$相连的边去掉后求一遍最小生成森林,并在$1$与每个连通块之间加入一条最小的边。如果$1$的度数大于$k$,则无解。否则需要做若干次操作,每次加入一条端点是$1$的边,并删掉形成的环上最大的边(为了使生成树最小),为了使生成树最小,每次操作的权值和增量需要最小。
主要思路就是这么简单,然而代码有些复杂。主要就是别把边在数组的下标和在原图的序号写混了,然后记得判无解,还有我把diredge edges[MAXM << 1]写成了diredge edges[MAXN << 1]导致$\texttt{RE}$,二十分钟才调出来。
还有,这题第一行输出边的数量,第二行输出的边在原图的序号,顺序任意。翻译里没写,我就自己猜的。
#include<cstdio>
#include<cstring>
#include<algorithm>
const int MAXN = 5010, MAXM = 100100;
int n, m, k, maxid[MAXN], maxw[MAXN], deg1, ccminid[MAXN], ccminw[MAXN], cnt;
bool inmst[MAXM];
struct undiredge {
int u, v, w, id;
bool operator < (const undiredge &a) const { return w < a.w; }
}edges[MAXM];
struct diredge { int to, next, w, id; };
struct graph {
int ecnt = 1, head[MAXN];
diredge edges[MAXM << 1];
inline void addedge(int u, int v, int w, int id) {
edges[++ecnt].to = v;
edges[ecnt].w = w;
edges[ecnt].id = id;
edges[ecnt].next = head[u];
head[u] = ecnt;
}
}g;
struct tools {
static inline void swap(int &a, int &b) { int t = a; a = b; b = t; }
static inline int max(int a, int b) { return a > b ? a : b; }
static inline int maxedge(int i, int j) { return g.edges[i].w > g.edges[j].w ? i : j; }
};
struct unionsetnode { int fa, size; };
struct unionset {
unionsetnode nodes[MAXN];
inline void init() {
for (int i = 1; i <= n; i++) nodes[i].fa = i, nodes[i].size = 1;
}
int find(int x) {
if (nodes[x].fa == x) return x;
return nodes[x].fa = find(nodes[x].fa);
}
inline void merge(int x, int y) {
x = find(x), y = find(y);
if (nodes[x].size < nodes[y].size) tools::swap(x, y);
nodes[y].fa = x;
nodes[x].size += nodes[y].size;
}
inline bool same(int x, int y) { return find(x) == find(y); }
}uset;
inline void kruskal() {
for (int i = 1; i <= m; i++) {
int &u = edges[i].u, &v = edges[i].v;
if (u == 1 || v == 1) continue;
if (!uset.same(u, v)) {
uset.merge(u, v);
inmst[edges[i].id] = true;
cnt++;
}
}
}
void dfs(int x, int maxidnow, int maxwnow, int lst) {
maxid[x] = g.edges[maxidnow].id;
maxw[x] = maxwnow;
for (int i = g.head[x]; i; i = g.edges[i].next) {
if (i == (lst ^ 1) || !inmst[g.edges[i].id]) continue;
int &t = g.edges[i].to, &w = g.edges[i].w;
if (x ^ 1) dfs(t, tools::maxedge(maxidnow, i), tools::max(maxwnow, w), i);
else dfs(t, maxidnow, maxwnow, i);
}
}
int main() {
scanf("%d%d%d", &n, &m, &k);
for (int i = 1; i <= m; i++) {
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
edges[i].u = u, edges[i].v = v, edges[i].w = w, edges[i].id = i;
g.addedge(u, v, w, i), g.addedge(v, u, w, i);
}
std::sort(edges + 1, edges + m + 1);
uset.init();
kruskal();
memset(ccminw, 0x3f, sizeof(int) * (n + 1));
for (int i = g.head[1]; i; i = g.edges[i].next) {
int t = uset.find(g.edges[i].to), &w = g.edges[i].w;
if (ccminw[t] > w) {
ccminw[t] = w;
ccminid[t] = g.edges[i].id;
}
}
for (int i = 1; i <= n; i++)
if (ccminid[i]) inmst[ccminid[i]] = true, deg1++, cnt++;
while (deg1 < k) {
dfs(1, 0, 0, 0);
int addid = 0, mindelta = 0x3fffffff, delid = 0;
for (int i = g.head[1]; i; i = g.edges[i].next) {
if (inmst[g.edges[i].id]) continue;
int &t = g.edges[i].to, &w = g.edges[i].w;
if (mindelta > w - maxw[t]) {
mindelta = w - maxw[t];
addid = g.edges[i].id;
delid = maxid[t];
}
}
if (!addid || !delid) break;
inmst[delid] = false;
inmst[addid] = true;
deg1++;
}
if (deg1 ^ k || cnt ^ (n - 1)) printf("-1\n");
else {
printf("%d\n", n - 1);
for (int i = 1; i <= m; i++)
if (inmst[i]) printf("%d ", i);
}
return 0;
}2020-07-18
黑暗城堡
先做一遍$\texttt{Dijkstra}$求最短路,然后对于边$(u,v)$,若$dis[u]+w=dis[v]$则说明这条边可行。做一个类似于$\texttt{Prim}$算法的过程,把节点按照$dis$从小到大排序,以保证$dis[x]>dis[t]$,$x$是当前要加入的节点,$t$是已加入且与$x$有边的节点。找到满足$dis[x]+w=dis[t]$的边的数量,然后根据乘法原理乘到答案里。
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
const int MOD = (1 << 31) - 1;
int n, m, dis[1010], nodes[1010], rank[1010];
bool vis[1010];
long long ans = 1;
struct edge {
int to, next, w;
};
struct graph {
int ecnt, head[1010];
edge edges[1000100];
inline void addedge(int u, int v, int w) {
edges[++ecnt].to = v;
edges[ecnt].w = w;
edges[ecnt].next = head[u];
head[u] = ecnt;
}
} g;
struct node {
int x, dist;
node(int xv = 0, int dv = 0) : x(xv), dist(dv) {}
bool operator<(const node &a) const { return dist > a.dist; }
};
std::priority_queue<node> q;
inline void dijkstra() {
q.push(node(1, 0));
memset(dis, 0x3f, sizeof(int) * (n + 1));
dis[1] = 0;
while (!q.empty()) {
node f = q.top();
q.pop();
if (vis[f.x])
continue;
vis[f.x] = true;
for (int i = g.head[f.x]; i; i = g.edges[i].next) {
int &t = g.edges[i].to, w = g.edges[i].w;
if (dis[t] > dis[f.x] + w) {
dis[t] = dis[f.x] + w;
q.push(node(t, dis[t]));
}
}
}
}
inline bool cmp(int &i, int &j) { return dis[i] < dis[j]; }
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
g.addedge(u, v, w), g.addedge(v, u, w);
}
dijkstra();
for (int i = 1; i <= n; i++) nodes[i] = i;
std::sort(nodes + 1, nodes + n + 1, cmp);
for (int i = 1; i <= n; i++) rank[nodes[i]] = i;
for (int i = 2; i <= n; i++) {
int x = nodes[i], cnt = 0;
for (int j = g.head[x]; j; j = g.edges[j].next) {
int &t = g.edges[j].to, &w = g.edges[j].w;
if (dis[x] == dis[t] + w && rank[t] < rank[x])
cnt++;
}
ans = (ans * cnt) % MOD;
}
printf("%lld\n", ans);
return 0;
}二分图最大匹配
https://www.luogu.com.cn/problem/P3386
对于每个节点从它出发找增广路,找到了就把增广路上的边取反,使得这个节点找到匹配点。因为前面的节点只会改变匹配点,不会失去匹配,所以从每个节点出发遍历一次就可以。
需要注意的是图的存储比较特别,只需要存从左部到右部的边,不需要存反向边。开的数组也是只需要开左部的大小。因为$\texttt{DFS}$时当前节点总是在左部,虽然边指向右部节点但直接就通过$\texttt{match}$数组跳到左部了。
#include<cstdio>
#include<cstring>
int n, m, e, ans, match[510];
bool vis[510];
struct edge { int to, next; };
struct graph {
int ecnt, head[510];
edge edges[50100];
inline void addedge(int u, int v) {
edges[++ecnt].to = v;
edges[ecnt].next = head[u];
head[u] = ecnt;
}
}g;
bool dfs(int x) {
vis[x] = true;
for (int i = g.head[x]; i; i = g.edges[i].next) {
int &t = g.edges[i].to;
if (vis[match[t]]) continue;
if (!match[t] || dfs(match[t])) {
match[t] = x;
return true;
}
}
return false;
}
int main() {
scanf("%d%d%d", &n, &m, &e);
for (int i = 1; i <= e; i++) {
int u, v;
scanf("%d%d", &u, &v);
g.addedge(u, v);
}
for (int i = 1; i <= n; i++) {
memset(vis, 0, sizeof(bool) * (n + 1));
if (dfs(i)) ans++;
}
printf("%d\n", ans);
return 0;
}棋盘覆盖
https://www.acwing.com/problem/content/description/374/
二分图匹配的两个要素:相同集合内没有边,每个节点只能匹配一个不同集合的点。把棋盘按照坐标和奇偶性分成两个集合,那么相邻的格子在不同的集合,可以在它们之间连边,在同一集合的点一定不相邻,也就没有边。连完边做一遍二分图最大匹配就可以了。
#include<cstdio>
#include<cstring>
const int dir[4][2] = { {1, 0}, {0, 1}, {-1, 0}, {0, -1} };
int n, p, ans;
bool able[110][110], vis[110][110];
struct state {
int x, y;
state(int xv = 0, int yv = 0): x(xv), y(yv) {}
bool operator ! () const { return x == 0 && y == 0; }
}match[110][110];
struct edge { state to; int next; };
struct graph {
int ecnt, head[110][110];
edge edges[40100];
inline void addedge(state u, state v) {
edges[++ecnt].to = v;
edges[ecnt].next = head[u.x][u.y];
head[u.x][u.y] = ecnt;
}
}g;
bool dfs(state x) {
vis[x.x][x.y] = true;
for (int i = g.head[x.x][x.y]; i; i = g.edges[i].next) {
state &t = g.edges[i].to;
if (vis[match[t.x][t.y].x][match[t.x][t.y].y]) continue;
if (!match[t.x][t.y] || dfs(match[t.x][t.y])) {
match[t.x][t.y] = state(x.x, x.y);
return true;
}
}
return false;
}
int main() {
scanf("%d%d", &n, &p);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) able[i][j] = true;
for (int i = 1; i <= p; i++) {
int x, y;
scanf("%d%d", &x, &y);
able[x][y] = false;
}
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
if ((i + j) % 2 || !able[i][j]) continue;
for (int k = 0; k < 4; k++) {
int xg = i + dir[k][0], yg = j + dir[k][1];
if (xg < 1 || xg > n || yg < 1 || yg > n || !able[xg][yg]) continue;
g.addedge(state(i, j), state(xg, yg));
}
}
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++) {
if ((i + j) % 2 || !able[i][j]) continue;
memset(vis, 0, sizeof vis);
if (dfs(state(i, j))) ans++;
}
printf("%d\n", ans);
return 0;
}[APIO2010]巡逻
https://www.luogu.com.cn/problem/P3629
求树的直径有两种方法。两次$\texttt{DFS}$,第一次随便选一个点找到最远的点,然后从找到的点在$\texttt{DFS}$一次找到最远的点,第一次找到的一定是直径的端点,而第二次找到的是直径。可以用反证法证明是正确的,但这种方法不适用于有负边权的情况。树形$\texttt{DP}$,状态是当前节点到子树的节点中最远的距离,然后当前子树的直径就是$dp_i+w_i+dp_j+w_j$,其中$i,j$是当前节点的两个子节点。不需要枚举$i,j$,在遍历子节点时用当前子节点加上之前遍历到的最远子节点就可以了,即$dp[x]+dp[t]+w$。然后答案在每个节点的子树的最长链中取$\max$,这样能够找到直径的原因是直径总会有一个最靠近根节点的顶点,所以直径总会在顶点处被枚举到,从而更新答案。可以用于有负边权的情况,但只能求数值不能求路径。
$k=1$时很简单,修出来的路可以让形成的环上本来要经过两次的边变成一次,于是直接找到直径然后在两个端点上修路就可以了。$k=2$时两个环的交集需要遍历两次,所以交集需要去掉。第一次需要在直径上修路,原因我也不知道,不会证明,我去问了$\texttt{wyh}$学长说应该是选非直径的情况可以转为选直径的情况且答案不会更劣(大概意思是这样),具体我还是不会证。找到直径后把直径上的边权变为$-1$,然后再求一遍直径,变为$-1$的作用是使找到的链与先前找到的直径有交集时答案更劣,也就是把交集去掉。
另外这题还有树形$\texttt{DP}$的做法,就是求两条最长不相交链。
#include<cstdio>
const int MAXN = 100100;
int n, k, maxdist, maxnode, from[MAXN], maxdist2, dp[MAXN];
struct edge { int to, next, w; };
struct graph {
int ecnt = 1, head[MAXN];
edge edges[MAXN << 1];
inline void addedge(int u, int v, int w) {
edges[++ecnt].to = v;
edges[ecnt].w = w;
edges[ecnt].next = head[u];
head[u] = ecnt;
}
}g;
struct tools { static int max(int a, int b) { return a > b ? a : b; } };
void dfs1(int x, int lst, int dist) {
if (dist >= maxdist) {
maxdist = dist;
maxnode = x;
}
for (int i = g.head[x]; i; i = g.edges[i].next) {
if (i == (lst ^ 1)) continue;
int &t = g.edges[i].to;
dfs1(t, i, dist + g.edges[i].w);
from[t] = x;
}
}
void dfs2(int x) {
for (int i = g.head[x]; i; i = g.edges[i].next) {
int &t = g.edges[i].to;
if (t == from[x]) {
g.edges[i].w = g.edges[i ^ 1].w = -1;
dfs2(t);
}
}
}
void dfs3(int x, int lst) {
for (int i = g.head[x]; i; i = g.edges[i].next) {
if (i == (lst ^ 1)) continue;
int &t = g.edges[i].to, w = g.edges[i].w;
dfs3(t, i);
maxdist2 = tools::max(maxdist2, dp[x] + w + dp[t]);
dp[x] = tools::max(dp[x], dp[t] + w);
}
}
int main() {
scanf("%d%d", &n, &k);
for (int i = 1; i < n; i++) {
int u, v;
scanf("%d%d", &u, &v);
g.addedge(u, v, 1), g.addedge(v, u, 1);
}
dfs1(1, 0, 0);
from[maxnode] = 0;
dfs1(maxnode, 0, 0);
dfs2(maxnode);
dfs3(1, 0);
if (k == 1) printf("%d\n", 2 * (n - 1) - maxdist + 1);
else printf("%d\n", 2 * n - maxdist - maxdist2);
return 0;
}2020-07-19
树网的核
https://www.luogu.com.cn/problem/P1099
关于树的直径有不少结论,虽然题目中给出了部分结论不过还是要证明一下。
- 任意节点距离最远的点一定是直径的端点。
设从点$P$出发,找到的最远的点是点$Q$,且$Q$不是直径的端点,$AB$为直径。
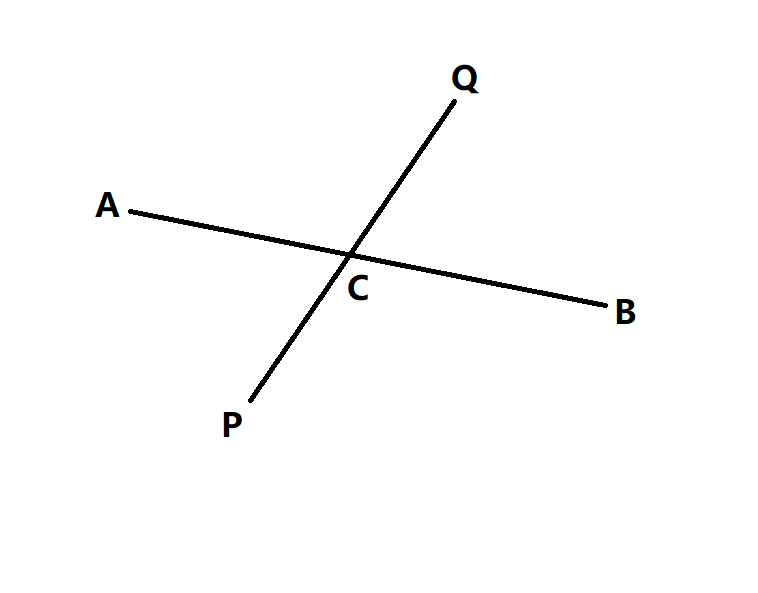
当$PQ$与$AB$相交时,设交于点$C$,因为找到的最远的点是$Q$所以$PC+CQ\ge PC+CA$,即$CQ\ge CA$,所以$CQ+BC\ge CA+BC$,即$CQ+BC\ge AB$,所以$BQ$一定是直径,$Q$为直径的端点,与条件矛盾。所以$Q$是直径的端点。
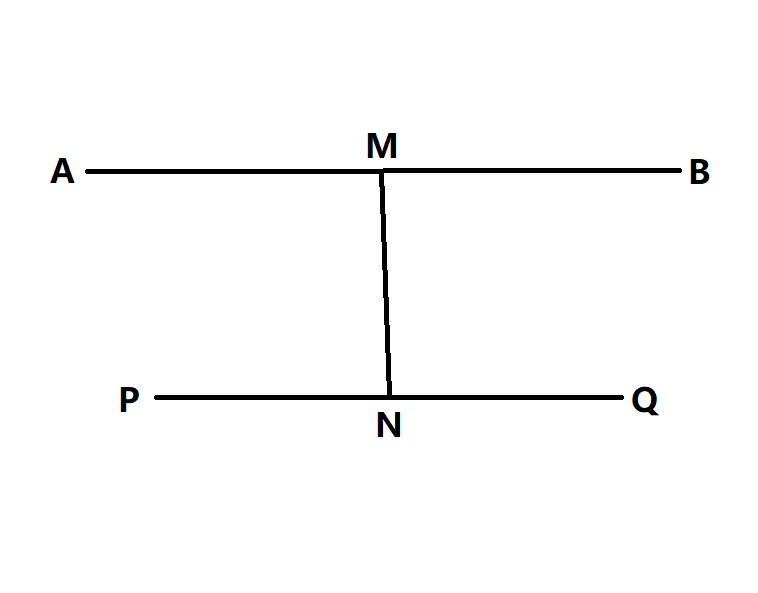
当$PQ$与$AB$不相交时,因为图是连通的所有肯定有一条路径$MN$把它们连起来,因为找到的最远的点是$Q$所以$PN+NQ\ge PN+NM+MA$,即$NQ\ge NM+MA$,所以$NQ-NM\ge MA$,所以$NQ+NM\ge MA$,即$BM+MN+NQ\ge BM+MA$,即$BQ\ge AB$,所以$BQ$一定是直径,$Q$为直径的端点,与条件矛盾。所以$Q$是直径的端点。
综上,任意节点距离最远的点一定是直径的端点。
参考资料:https://blog.csdn.net/forever_dreams/article/details/81051578
- 若树有多条直径,它们一定相交。

若$AB$、$PQ$都是直径,且它们不相交,因为图是连通的所以肯定有一条路径$MN$把它们连起来,选择$AM,BM,PN,QN$中最长的两条加上$MN$,显然可以组成大于直径的路径,与条件矛盾,所以直径一定相交。
- 若树有多条直径,它们的非公共部分的两端分别相等。
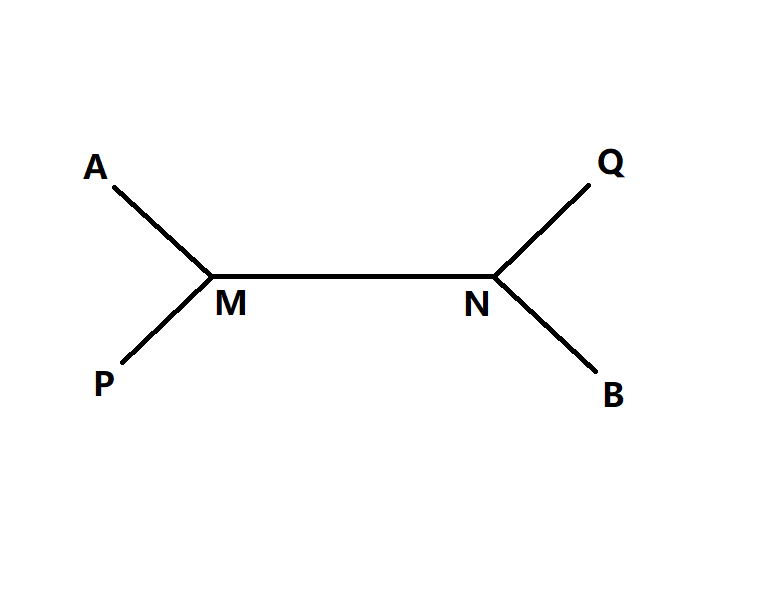
若$AB,PQ$都是直径,且它们的公共部分为$MN$,两端的非公共部分长度分别不相等。分别选择两端最长的再加上$MN$,显然可以组成大于直径的路径,与条件矛盾,所以多条直径的非公共部分两端分别相等。
- 若树有多条直径,它们的中点相同。
由上面的结论可以推出。
- 使偏心距最小的路径一定是直径的一部分。
可以把路径抽象为一个点,离这个点最远的点是直径的端点,所以这个点离直径越近偏心距越小,这个点在直径中点上时偏心距最小。
- 若树有多条直径,从任意一条直径上求最小偏心距都是等价的。
设直径上有$t$个节点,把直径上第$i$个点记为$u_i$,把直径上每个点不经过直径上的节点,能够到达的最远的距离记为$d[u_i]$。则一段从$u_i$到$u_j$的路径的偏心距为$\max(\max_{k=i}^{j}d[u_k],dist(u_1,u_i),dist(u_j,u_t))$。由直径的最长性可知,那些在直径上但不在路径上的点的$d$对答案没有贡献,所以上式等于$\max(\max_{k=1}^{t}d[u_k],dist(u_1,u_i),dist(u_j,u_t))$。也就是说,一条路径的偏心距等于直径的偏心距和路径端点到直径端点的距离的最大值。
因为有多条直径,所以图是这样的形状:

其中$PQ$、$AB$都是直径,$MN$是它们的公共部分(可能只有一个点,也可能是一条路径,不影响证明),其他边略去。设我们选的直径是$PQ$。由直径的最长性可知$PM,QN$上的节点(点$M$、点$N$除外,下文相同)的 $d$分别不会大于$PM,QN$,而$PM=AM,QN=BN$,所以它们分别不会大于$AM,BN$,而$AM,BN$分别是点$M$和点$N$的$d$值,所以$PM,QN$上的点的$d$对答案没有贡献。所以$PQ$的偏心距是路径$MN$上$d$的最大值,对于$AB$也是如此,所以多条直径的偏心距相同。
要使$dist(u_1,u_i)$对答案产生贡献,必然有$dist(u_1,u_i)>\max(AM,BN)$。因此,点$u_i$在路径$MQ$上。但我们的目的是使偏心距最小,如果点$u_i$在$NQ$上显然不如在$MN$上优,所以点$u_i$应当在$MN$上。当然也有可能$\max(AM,BN)>PN$,这时候点$u_i$就必须在$NQ$上,但这样求出来的不是最小偏心距,所以无需考虑。设点$u_i$在$MN$上的位置是点$C$,因为$PM+MC=AM+MC$所以$dist(u_1,u_i)$在不同的直径上相等。$dist(u_j,u_t)$同理,因此,要使后两个值对答案产生贡献,它们在不同的直径上必然相等,否则就算不相等对答案也没有贡献,不用去管它。
综上所述,在不同的直径上求出的最小偏心距是相等的。
参考资料:https://www.codetd.com/article/7651409 。不过我感觉资料中对于推论的证明有错误。我的证明我也不能保证是正确的。
根据上面的证明我们可以直接在直径上用双指针以$O(n)$的复杂度枚举路径,然后算答案。
#include<cstdio>
#include<vector>
int n, s, maxdis, maxnode, from[310], diaecc, fromw[310], ans = 0x3fffffff;
bool indiameter[310];
struct edge { int to, next, w; };
struct graph {
int ecnt = 1, head[310];
edge edges[610];
inline void addedge(int u, int v, int w) {
edges[++ecnt].to = v;
edges[ecnt].w = w;
edges[ecnt].next = head[u];
head[u] = ecnt;
}
}g;
std::vector<int> diameter;
struct tools {
static inline int max(int a, int b) { return a > b ? a : b; };
static inline int min(int a, int b) { return a < b ? a : b; };
};
void dfs1(int x, int lst, int dis) {
if (maxdis < dis) {
maxdis = dis;
maxnode = x;
}
for (int i = g.head[x]; i; i = g.edges[i].next) {
if (i == (lst ^ 1)) continue;
int &t = g.edges[i].to;
from[t] = x;
fromw[t] = g.edges[i].w;
dfs1(t, i, dis + g.edges[i].w);
}
}
void dfs2(int x) {
if (!x) return;
indiameter[x] = true;
diameter.push_back(fromw[x]);
dfs2(from[x]);
}
void dfs3(int x, int lst, int dis) {
if (indiameter[x]) dis = 0;
else diaecc = tools::max(diaecc, dis);
for (int i = g.head[x]; i; i = g.edges[i].next) {
if (i == (lst ^ 1)) continue;
int &t = g.edges[i].to;
dfs3(t, i, dis + g.edges[i].w);
}
}
int main() {
scanf("%d%d", &n, &s);
for (int i = 1; i < n; i++) {
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
g.addedge(u, v, w), g.addedge(v, u, w);
}
dfs1(1, 0, 0);
from[maxnode] = fromw[maxnode] = maxdis = 0;
dfs1(maxnode, 0, 0);
dfs2(maxnode);
dfs3(maxnode, 0, 0);
int l = 0, r = 0, len = 0, ldis = 0, rdis = maxdis;
while (r + 1 <= (int)diameter.size() - 1 && len + diameter[r] <= s) rdis -= diameter[r], len += diameter[r], r++;
while (l <= (int)diameter.size() - 1) {
ans = tools::min(ans, tools::max(diaecc, tools::max(ldis, rdis)));
ldis += diameter[l], len -= diameter[l], l++;
while (r + 1 <= (int)diameter.size() - 1 && len + diameter[r] <= s) rdis -= diameter[r], len += diameter[r], r++;
}
printf("%d\n", ans);
return 0;
}异象石
把各点按照遍历到的时间戳排成一圈,各点之间的边集的边权和的两倍就等于相邻的节点的距离的和。这个还是挺好理解的,我就不证明了。用$\texttt{set}$维护从小到大排序的点集,然后增删节点时把答案对应地加减。
十分sb地把点到根的距离作为深度用在$\texttt{lca}$里面了,花了一小时多才调出来。点到根的距离和点到根经过的边数要分清。
#include<cstdio>
#include<set>
const int MAXN = 100100;
int n, m, f[MAXN][21], dfn[MAXN], cnt, depth[MAXN];
long long dis[MAXN], ans;
struct edge { int to, next, w; };
struct graph {
int ecnt = 1, head[MAXN];
edge edges[MAXN << 1];
inline void addedge(int u, int v, int w) {
edges[++ecnt].to = v;
edges[ecnt].w = w;
edges[ecnt].next = head[u];
head[u] = ecnt;
}
}g;
struct tools {
static inline void swap(int &a, int &b) { int t = a; a = b; b = t; }
};
struct node {
int x;
node(int xv = 0): x(xv) {}
bool operator < (const node &a) const { return dfn[x] < dfn[a.x]; }
};
std::set<node> nodes;
void dfs1(int x, int fa, int lst, long long dist) {
depth[x] = depth[fa] + 1;
f[x][0] = fa;
dfn[x] = ++cnt;
dis[x] = dist;
for (int i = 1; i <= 20; i++) f[x][i] = f[f[x][i - 1]][i - 1];
for (int i = g.head[x]; i; i = g.edges[i].next) {
if (i == (lst ^ 1)) continue;
int &t = g.edges[i].to;
dfs1(t, x, i, dist + g.edges[i].w);
}
}
inline int lca(int x, int y) {
if (depth[x] < depth[y]) tools::swap(x, y);
for (int i = 20; i >= 0; i--)
if (depth[f[x][i]] >= depth[y]) x = f[x][i];
if (x == y) return x;
for (int i = 20; i >= 0; i--)
if (f[x][i] ^ f[y][i]) x = f[x][i], y = f[y][i];
return f[x][0];
}
inline long long dist(int x, int y) { return dis[x] + dis[y] - dis[lca(x, y)] * 2; }
inline void insert(int x) {
std::set<node>::iterator p = nodes.insert(node(x)).first;
std::set<node>::iterator l = (p == nodes.begin()) ? --nodes.end() : --nodes.find(node(x));
std::set<node>::iterator r = (p == --nodes.end()) ? nodes.begin() : ++nodes.find(node(x));
ans -= dist(l -> x, r -> x);
ans += dist(l -> x, p -> x) + dist(p -> x, r -> x);
}
inline void remove(int x) {
std::set<node>::iterator p = nodes.find(node(x));
std::set<node>::iterator l = (p == nodes.begin()) ? --nodes.end() : --nodes.find(node(x));
std::set<node>::iterator r = (p == --nodes.end()) ? nodes.begin() : ++nodes.find(node(x));
ans -= dist(l -> x, p -> x) + dist(p -> x, r -> x);
ans += dist(l -> x, r -> x);
nodes.erase(p);
}
int main() {
scanf("%d", &n);
for (int i = 1; i < n; i++) {
int u, v, w;
scanf("%d%d%d", &u, &v, &w);
g.addedge(u, v, w), g.addedge(v, u, w);
}
dfs1(1, 0, 0, 0);
scanf("%d", &m);
while (m--) {
char opt = getchar();
while ((opt ^ '+') && (opt ^ '-') && (opt ^ '?')) opt = getchar();
if (opt == '+') {
int x;
scanf("%d", &x);
insert(x);
}
else if (opt == '-') {
int x;
scanf("%d", &x);
remove(x);
}
else if (opt == '?') printf("%lld\n", ans / 2);
}
return 0;
}